I recently completed a semester of studying stochastic predator prey systems and I wanted to take the time to explain the basics of what such a thing is. The aim is the provided an explanation that is not rigorous but more in layman’s terms. So how do we go from:

\(\begin{array}{c} \frac{d x}{d t}=\alpha x-\beta x y \\ \frac{d y}{d t}=\delta x y-\gamma y \end{array}\)

to:

(I promise that this is not random… well not entirely)

The system of equations is better known as the Lotka-Volterra Equations and explains the relationship between 2 species: x which is prey, and y which is a predator. The real parameters: \(\alpha, \beta, \gamma \text{and } \delta\) describe how these two species interact with each other. The govern things like prey reproduction (\(\alpha\)) and chance of being eaten \(\beta\). They are also usually one of the first introductions to nonlinear dynamics which is a frequent interest in so many fields. This system is great to understand and study but what if you wanted to introduce another species or you want to change one of the parameters in a specific region? A cheetah would have a much more difficult time in a jungle than in its natural savanna habitat. This is where the simulation work comes into play.

We first want to set up a system that is easy to work with. This can be done in a few different ways but we will construct a lattice that is topologically isomorphic to a torus. Essentially. we want to avoid serious boundary problems. We do this by imagining a chessboard and placing a king on the board. The king can move to any of the 4 adjacent tiles for every time step. We want to king to always be able to move to 4 possible tiles but what if the king is on the far left of the board? If the king were to move left of this they would end up on the far right side of the board. Similarly, if the king is at the zenith of the board, if it moved up it would be placed at the very bottom of the board. This way, the board kind of acts like a torus with the pieces never falling off of the board.

There are also different types of iterations that creatures can have with each other. For our purposes, we will assume that the species will prey on each other in a cyclic process. That is, if we have 3 creatures: A will eat B, B will eat C and C will eat A. A point can also not be occupied by any creature, which we will arbitrarily label as D and not have any possible interaction for this “type”. We can of course expand this to any number of species, we just change the first and last prey relationship.

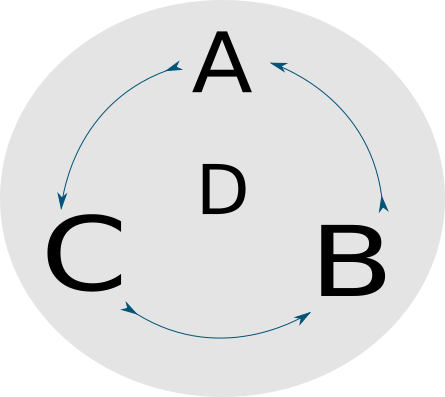
We now that we have a predator prey relationship and a space to use we also need to define the types of actions that these species can preform. Similarly to the Lotka-Volterra model we allow for 4 actions: death, predation, movement, reproduction. These actions are governed by the real parameters: \(\mu ,\lambda , D,\text{and }\sigma\). These parameters now determine if an action if successful.

All of this produces the following gif of a 3 species Predator-Prey with black as empty:

My particular implementation can be found here: Get the Git!. Essentially, there is a time loop to govern the number of interactions, a random lattice location is selected using the Mersene Twister then a random action is selected, it checks to see if the action succeeds and updates the lattice accordingly.